Chap 1 - Introduction
What is Machine Learning?
Definition by Arthur Samuel(1959): “Field of study that gives computers the ability to learn without being explicitly programmed.”
Definition by Tom Mitchell(1998): “A computer program is said to learn form experience E with
respect to some task T and some performance measure P, if its performance on T, as measured by P,
improves with experience E.”
In general, any ML problem can be assigned to one of two broad classification: supervised learning or unsupervised learning.
Supervised Learning
- Supervised learning is the ML task of learning a way to map input signals to output values by training a model on a
set of training examples where each example is a pair consisting of an input and a desired output value.
- Alternatively, we know the relationship between the input and output.
- Regression Problem: try to predict results within a continuous output (ie, map input variables to some continuous function)
- E.g. House Price Prediction
- Classification Problem: try to predict results in a discrete output (ie, map input variables into discrete categories)
- E.g. Cancer Categorization (malignant/benign tumor), Email spam/not spam.
Unsupervised Learning
- Unsupervised ML is the ML task of inferring a function to describe hidden structure from “unlabeled” data.
Examples of unsupervised learning tasks include clustering (where we try to discover underlying groupings of examples)
and anomaly detection (where we try to infer if some examples in a dataset do not conform to some expected pattern).
- Alternatively, we have little or no idea what our results should look like.
- There is no feedback based on the prediction results with unsupervised learning.
- E.g.: Orgnize computing clusters, Social network analysis, Market segmentation, Astronomical data analysis
- Clustering Problem Example: Automatically group a huge amount of genes into groups that are somehow similar or related by different variables, such as lifespan, location, roles, and so on.
- Non-clustering Problem Example: The “Cocktail Party Algorithm”, allows you to find structure in a chaotic environment.
- Source separation: Cocktail party problem
[W,s,v]=svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x'); - GNU Octave, a great PL for algorithm prototyping
- Source separation: Cocktail party problem
Model and Cost Function
Model Representation
In regression problems, we are taking input variables and trying to fit the output onto a continuous expected result function.
Linear regression with one variable is also known as “univariate linear regression.”
Univariate linear regression is used when predicts a single output value y from a single input value x.
Notation
- \(m\) = number of training examples
- \(x's\) = “input” variable / features
- \(y's\) = “output” variable / “target” variable
- \((x, y)\) = one training example
- \((x^{(i)}, y^{(i)}) = i^{(th)}\) training example
- \(\theta_i = i^{th}\) parameter of model
Hypothesis function: \(\hat{y} = h_\theta(x) = \theta_0 + \theta_1 x\)
Note that this is like the equation of a straight line. We give to \(h_\theta(x)\) values for \(\theta_0\) and \(\theta_1\) to get our estimated output \(\hat{y}\). In other words, we are trying to create a function called \(h_\theta\) that is trying to map our input data (the \(x's\)) to the output data (the \(y's\)))
Parameter Learning
Cost Function
The accuracy of hypothesis function can be measured by a cost function. This takes an “average” of all the results of the hypothesis with inputs from \(x's\) compared to the actual output \(y's\).
Cost Function: \(J(\theta_0, \theta_1) = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left ( \hat{y}_{i}- y_{i} \right)^2 = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left (h_\theta (x_{i}) - y_{i} \right)^2\)
This function is also known as “Squared Error Function”. - Please refer to Squared Error Function (aka, Mean squared error)
Gradient Descent
After having a hypothesis function and a cost function to measure hypothesis function, now we uses Gradient Descent to estimate the parameters in hypothesis function.
Imagine that we graph our hypothesis function based on its fields \(\theta_0\) and \(\theta_1\) (actually we are graphing the cost function as a function of the parameter estimates). This can be kind of confusing; we are moving up to a higher level of abstraction. We are not graphing x and y itself, but the parameter range of our hypothesis function and the cost resulting from selecting particular set of parameters.
We put \(\theta_0\) on the x axis and \(\theta_1\) on the y axis, with the cost function on the vertical z axis. The points on our graph will be the result of the cost function using our hypothesis with those specific theta parameters.
We will know that we have succeeded when our cost function is at the very bottom of the pits in our graph, i.e. when its value is the minimum.
The way we do this is by taking the derivative (the tangential line to a function) of our cost function. The slope of the tangent is the derivative at that point and it will give us a direction to move towards. We make steps down the cost function in the direction with the steepest descent, and the size of each step is determined by the parameter \(\alpha\), which is called the learning rate.
The gradient descent algorithm is:
\(\begin{align*}
\text{repeat until convergence: } \lbrace & \newline
\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1) \newline
\rbrace&
\end{align*}\)
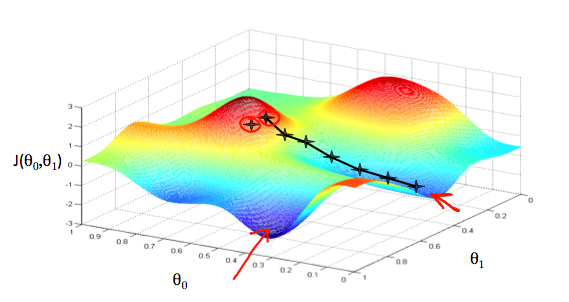
Gradient Descent for Linear Regression
Algorithm:
\(\begin{align*}
\text{repeat until convergence: } \lbrace & \newline
\theta_0 := & \theta_0 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m}(h_\theta(x_{i}) - y_{i}) \newline
\theta_1 := & \theta_1 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m}\left((h_\theta(x_{i}) - y_{i}) x_{i}\right) \newline
\rbrace&
\end{align*}\)
Facts
- “Batch” Gradient Descent: Each step of gradient descent uses all the training examples.
- Gradient descent can converge even if \(\alpha\) is kept fixed. (But \(\alpha\) cannot be too large, or else it may fail to converge).
- For the specific choice of cost function J used in linear regression, there are no local optima (other than the global optimum).
Chap 2 - Linear Regression with Multiple Variables
Linear regression with multiple variables is also known as “multivariate linear regression”.
We now introduce notation for equations where we can have any number of input variables.
\[\begin{align*}x_j^{(i)} &= \text{value of feature } j \text{ in the }i^{th}\text{ training example} \newline x^{(i)}& = \text{the column vector of all the feature inputs of the }i^{th}\text{ training example} \newline m &= \text{the number of training examples} \newline n &= \left| x^{(i)} \right| ; \text{(the number of features)} \end{align*}\]Now define the multivariable form of the hypothesis function as follows, accommodating these multiple features:
\(h_\theta (x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3 + \cdots + \theta_n x_n\)
In order to develop intuition about this function, we can think about \(\theta_0\) as the basic price of a house, \(\theta_1\) as the price per square meter, \(\theta_2\)as the price per floor, etc. \(x_1\) will be the number of square meters in the house, \(x_2\) the number of floors, etc.
Using the definition of matrix multiplication, our multivariable hypothesis function can be concisely represented as:
\(\begin{align*}h_\theta(x) =\begin{bmatrix}\theta_0 \hspace{2em} \theta_1 \hspace{2em} ... \hspace{2em} \theta_n\end{bmatrix}\begin{bmatrix}x_0 \newline x_1 \newline \vdots \newline x_n\end{bmatrix}= \theta^T x\end{align*}\)
Remark: Note that for convenience reasons in this course Mr. Ng assumes \(x_{0}^{(i)} =1 \text{ for } (i\in { 1,\dots, m } )\)
The training examples are stored in X row-wise, like such:
\(\begin{align*}X = \begin{bmatrix}x^{(1)}_0 & x^{(1)}_1 \newline x^{(2)}_0 & x^{(2)}_1 \newline x^{(3)}_0 & x^{(3)}_1 \end{bmatrix}&,\theta = \begin{bmatrix}\theta_0 \newline \theta_1 \newline\end{bmatrix}\end{align*}\)
You can calculate the hypothesis as a column vector of size (m x 1) with: \(h_\theta(X) = X \theta\)
For the rest of these notes, \(X\) will be represent a matrix of training examples \(x_(i)\) stored row-wise.
Cost Function
For the parameter \(\theta\) (of type \(\mathbb{R}^{(n+1)}\)or \(\mathbb{R}^{(n+1) \times 1}\)),
cost function: \(J(\theta) = \dfrac {1}{2m} \displaystyle \sum_{i=1}^m \left (h_\theta (x^{(i)}) - y^{(i)} \right)^2\)
The vectorized version: \(J(\theta) = \dfrac {1}{2m} (X\theta - \vec{y})^{T} (X\theta - \vec{y})\)
Gradient Descent for Multiple Variables
The gradient descent equation itself is generally the same form; we just have to repeat it for our ‘n’ features:
\(\begin{align*}
& \text{repeat until convergence:} \; \lbrace \newline
\; & \theta_0 := \theta_0 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_0^{(i)}\newline
\; & \theta_1 := \theta_1 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_1^{(i)} \newline
\; & \theta_2 := \theta_2 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_2^{(i)} \newline
& \cdots
\newline \rbrace
\end{align*}\)
In other words:
\(\begin{align*}& \text{repeat until convergence:} \; \lbrace \newline \; & \theta_j := \theta_j - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \; & \text{for j := 0..n}\newline \rbrace\end{align*}\)
Matrix Notation
The Gradient Descent rule can be expressed as:
\(\theta := \theta - \alpha \nabla J(\theta)\)
where \(\nabla J(\theta)\) is a vector of the form:
\(\nabla J(\theta) = \begin{bmatrix}\frac{\partial J(\theta)}{\partial \theta_0} \newline \frac{\partial J(\theta)}{\partial \theta_1} \newline \vdots \newline \frac{\partial J(\theta)}{\partial \theta_n} \end{bmatrix}\)
The j-th component of the gradient is the summation of the product of two terms:
\(\begin{align*}
\; &\frac{\partial J(\theta)}{\partial \theta_j} &=& \frac{1}{m} \sum\limits_{i=1}^{m} \left(h_\theta(x^{(i)}) - y^{(i)} \right) \cdot x_j^{(i)} \newline
\; & &=& \frac{1}{m} \sum\limits_{i=1}^{m} x_j^{(i)} \cdot \left(h_\theta(x^{(i)}) - y^{(i)} \right)
\end{align*}\)
Sometimes, the summation of the product of two terms can be expressed as the product of two vectors.
Here, \(x_j^{(i)}\) for i = 1, 2, … m, represents the m elements of the j-th columns, \(\vec{x_j}\), of the training set X.
The other term \(\left(h_\theta(x^{(i)}) - y^{(i)} \right)\) is the vector of the deviation between the prediction
\(h_\theta(x^{(i)})\) and the true values \(y^{(i)}\). Rewriting \(\frac{\partial J(\theta)}{\partial \theta_j}\), we have:
The vectorized matrix notation: \(\theta := \theta - \frac{\alpha}{m} X^{T} (X\theta - \vec{y})\)
Feature Normalization
We can speed up gradient descent by having each of our input values in roughly the same range. This is because \(\theta\) will descend quickly on small ranges and slowly on large ranges, and so will oscillate inefficiently down to the optimum when the variables are very uneven.
The way to prevent this is to modify the ranges of our input variables so that they are all roughly the same. Ideally:
−1 ≤ \(x_(i)\) ≤ 1 or −0.5 ≤ \(x_(i)\) ≤ 0.5
These aren’t exact requirements; we are only trying to speed things up. The goal is to get all input variables into roughly one of these ranges, give or take a few.
Two techniques to help with this are feature scaling and mean normalization. Feature scaling involves dividing the input values by the range (i.e. the maximum value minus the minimum value) of the input variable, resulting in a new range of just 1. Mean normalization involves subtracting the average value for an input variable from the values for that input variable, resulting in a new average value for the input variable of just zero. To implement both of these techniques, adjust your input values as shown in this formula:
\[x_i := \dfrac{x_i - \mu_i}{s_i}\]Where \(μ_i\) is the average of all the values for feature (i) and \(s_i\) is the range of values (max - min), or \(s_i\) is the standard deviation.
Note that dividing by the range, or dividing by the standard deviation, give different results. The quizzes in this course use range - the programming exercises use standard deviation.
Example: xi is housing prices with range of 100 to 2000, with a mean value of 1000. Then, \(x_i := \dfrac{price-1000}{1900}\)
Gradient Descent Tips
- Debugging gradient descent: Make a plot with number of iterations on the x-axis. Now plot the cost function, \(J(\theta)\) over the number of iterations of gradient descent. If \(J(\theta)\) ever increases, then you probably need to decrease \(\alpha\).
- Automatic convergence test: Declare convergence if \(J(\theta)\) decreases by less than E in one iteration, where E is some small value such as \(10^{-3}\). However in practice it’s difficult to choose this threshold value.
It has been proven that if learning rate \(\alpha\) is sufficiently small, then \(J(\theta)\) will decrease on every iteration. Andrew Ng recommends decreasing \(\alpha\) by multiples of 3.
Features and Polynomial Regression
We can improve our features and the form of our hypothesis function in a couple different ways.
We can combine multiple features into one. For example, we can combine \(x_1\) and \(x_2\) into a new feature \(x_3\) by taking \(x_1⋅x_2\).
Polynomial Regression Our hypothesis function need not be linear (a straight line) if that does not fit the data well.
We can change the behavior or curve of our hypothesis function by making it a quadratic, cubic or square root function (or any other form).
For example, if our hypothesis function is \(h_\theta(x) = \theta_0 + \theta_1 x_1\) then we can create additional features based on \(x_1\), to get the quadratic function \(h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_1^2\) or the cubic function \(h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_1^2 + \theta_3 x_1^3\). In the cubic version, we have created new features \(x_2 = x_1^2\) and \(x_3 = x_1^3\).
To make it a square root function, we could do: \(h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 \sqrt{x_1}\)
One important thing to keep in mind is, if you choose your features this way then feature scaling becomes very important.
eg. if \(x_1\) has range 1 - 1000 then range of \(x_1^2\) becomes 1 - 1000000 and that of \(x_1^3\) becomes 1 - 1000000000.
Normal Equation
The “Normal Equation” is a method of finding the optimum theta without iteration:
\(\theta = (X^T X)^{-1}X^T y\)
Remark: There is no need to do feature scaling with the normal equation. Mathematics proofs: link 1, link 2.
The following is a comparison of gradient descent and the normal equation:
| Gradient Descent | Normal Equation |
|---|---|
| Need to choose \(\alpha\) | No need to choose \(\alpha\) |
| Need many iterations | No need to iterate |
| \(O(kn^2)\) | \(O(n^3)\), need to calculate inverse of \(X^TX\) |
| Works well when n is large | slow if n is large |
Remark: \(n \approx 10000\)
Normal Equation Non-invertibility
When implementing the normal equation in octave we want to use the ‘pinv’ function rather than ‘inv.’ \(X^TX\) may be non-invertible. The common causes are:
- Redundant features, where two features are very closely related (i.e. they are linearly dependent)
- Too many features (e.g. \(m \leq n\)). In this case, delete some features or use “regularization” (to be explained in a later lesson).